UFJF | FACULDADE DE ECONOMIA | ECONS

LABORATÓRIO DE ESTUDOS ECONÔMICOS
Introdução ao R - ECONS
André Suriane; Stephanie M.P. da Costa.
Antes de começar¶
Por que usar o R?
- Livre e Gratuito;
- Não serve somente para econometria/estatística;
- Automatizar/repetir procedimentos;
- Similiaridade e associação com outras linguagens de programação;
- Facilidade de divulgar/dividar resultados com outros programas e formatos (LATEX, Shiny, PDF, MarkDown, Jupyter(HTML, GIT, ipynb,doc) ...);
- Quantidade, diversidade e qualidade dos pacotes;
- Tamanho da comunidade;
- Facilidade de encontrar suporte na web;
- Pacotes e funções são atualizados constantemente;
- Mercado de trabalho (grandes empresas estão cada vez mais interessados em prossionais que saibam usar R);
- Te obriga a ter um conhecimento teórico maior;
- Conversa com outros softwares;
- Liberdade na implementação e criação de scripts.
quais são os custos?
- iniciação difícil;
- necessidade de aprofundamento computacional para execução das tarefas;
1 Introdução¶
Este curso tem um perfil de introdutório de manipulação, análise e apresentação gráfica de dados. O objetivo deste curso é capacitar o usuário a visualizar, manipular e analisar dados no R a partir da compreensão da estrutura e funcionamento do software. Para isso são apresentados a operacionalização do R e algumas funções básicas, como manipular bancos de dados, melhorar a "aparência" dos dados, modificar e criar variáveis, calcular estatísticas descritivas e criar apresentações gráficas dos dados.
O curso está dividido em duas partes:
na primeira será mostrado a operacionalização do R, com funções e manipulação e definição de objetos. O foco é garantir ao aluno conhecimento que permita ele ingressar no uso do software sem maiores barreiras; a segunda parte, foca em mostrar elementos básicos da análises estatística e econômica no R.
Para mais informações acesse a página do ECONS (www.ufjf.br/econs/).
1.1 Instalando o R¶
O R é um software livre para computação estatística e construção de gráficos que pode ser baixado e distribuído gratuitamente de acordo com a licença GPL. O R está disponível para as plataformas UNIX, Windows e MacOS.
Windows - Instalação rápida¶
- baixe a última versão do aplicativo no link, e execute seguindo as observações para instalação.
http://cran-r.c3sl.ufpr.br/bin/windows/base/
Interface R no sistema operacional Windows¶
Linux - distribuição Ubuntu¶
- Execute em um terminal
Ubuntu
sudo apt-get install r-base r-base-core
Fedora/RHEL/CENTOS
sudo yum install R
Obs: Entre em http://cran-r.c3sl.ufpr.br/bin/linux e veja as instruções específicas para sua distribuição. As distribuições que já possuem pacotes pré-compilados são: Debian(Ubuntu), RedHat(CentOS), Fedora, Suse(OpenSuse).
Interface R no sistema operacional Linux - Ubuntu¶
1.2 Interface do R¶
Fazer dowload no link: https://www.rstudio.com/products/rstudio/download/
Escolher a ultima versão do RStudio para instalar, lembrando sempre que pode haver versões novas.
Interface do RStudio¶
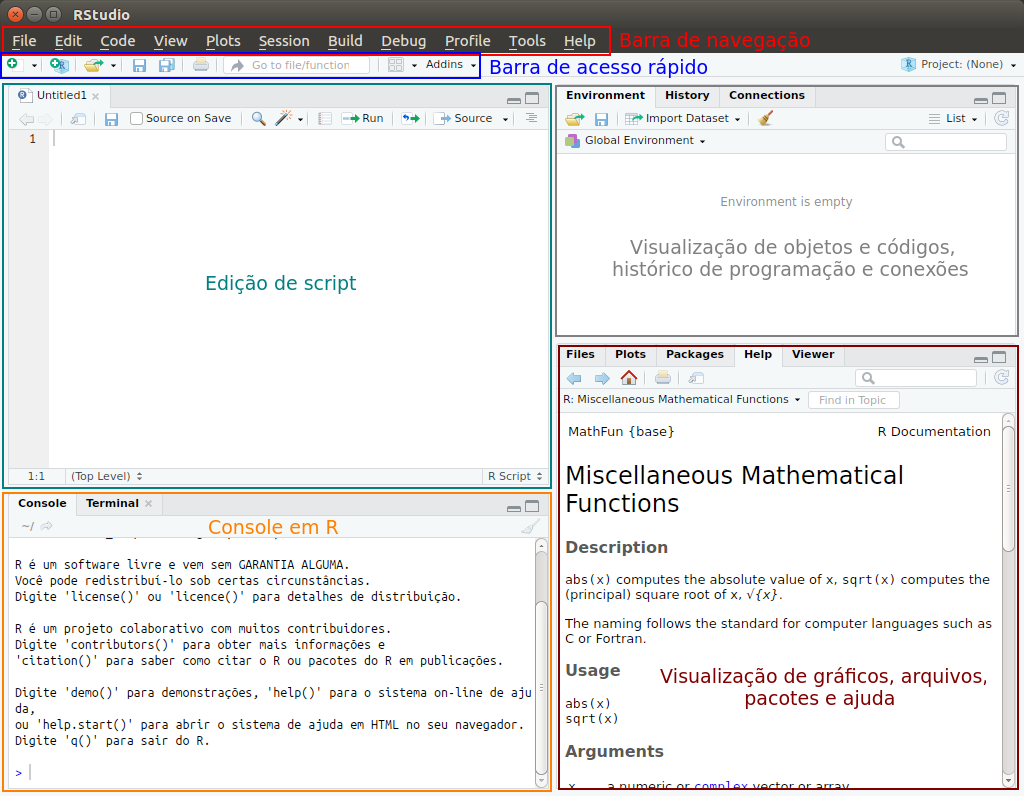
help(comando) # sintaxe
help(sqrt)
help("sqrt") #ajuda sobre o comando de raiz quadrada
?sqrt
help.search("sqrt")
Ao executar o exemplo acima no R, uma interface do menu de ajuda será executada mostrando o tópico da função sqrt, que é função matemática para a raiz quadrada.
Exemplo da descrição de ajuda para a função sqrt.

Para conhecer e tirar dúvidas sobre o R acesse:
2.2 Pacotes¶
O R conta com uma infinidade de pacotes permitindo o usuário as mais diversificadas ações.
Para installar um pacote use install.packages("pkg.name") ou use o painel do RStudio (Packages/Install).
Exemplo:
install.packages("ggplot2")
Pacotes úteis
| Nome | Descrição |
|---|---|
| Manipulação de dados | |
| dplyr* | manipulação de dados |
| feather | Abrir e salvar dados de forma eficiente |
| foreign* | Importar e exportar bases de/para outros programas |
| haven* | Importar e exportar bases de/para outros programas |
| DBI | Conectar com bases de dados |
| filehash | Alocar memoria em HD para grandes bases de dados |
| RSQLite | Conectar com bases SQLite (requer DBI) |
| tidyverse | Data science |
| Gráficos | |
| ggplot2* | Criar manipular gráficos |
| ggfortify* | Gráficos para resultados de modelos |
| ggcorrplot* | Gráfico de correlações |
| grid | Combinar, criar arranjos gráficos |
| lattice | alternativa ao contour plot |
| viridis* | Paleta de cores alternativa |
| plotly | Criar manipular gráficos |
| Exportar resultados em LaTeX ou HTML | |
| Hmisc | Exportar em LATEX ou HTML e outras funções |
| xtable | Exportar em LATEX ou HTML |
| Algebra | |
| Matrix | Operações com Matrizes |
| Rfast | Funções eficientes de manipulação algebrica |
| Estatística | |
| survival | Regressões censuradas |
| systemfit | Sistema de Equações |
| MASS | Várias funções estatísticas |
| MVar.pt* | Análise multivariada com saídas em português |
| nlme | Efeitos fixos e Aleatórios |
| nls2 | Regressões não lineares |
| nnet | Multinomial logit/probit |
| Acesso a Dados | |
| Quandl | Acesso a dados financeiros e econômicos em geral |
| quantmod | Acesso e ferrementas dados financeiros e econômicos em geral |
| BatchGetSymbols | Acesso a dados financeiros |
| BETS | Dados macroecônomicos do Brasil |
| microdadosBrasil | Microdados do Brasil |
| lodown | Microdados produzindos no mundo |
*devem ser instaladas para o curso de introdução.
Para ter acesso as funções de pacote deve usar a função:
library(pacname) ou require(pacname)
Pelo RStudio basta selecionar o pacote pela janela Packages.
2.3 Atribuição de Valores¶
Como todo tipo de programação, é comum que tenhamos que atribuir valores para algumas variáveis antes de utilizá-las. No R podemos fazer uma atribuição de valores de várias formas, conforme os exemplos abaixo:
x <- 5 # x recebe o valor 5
x = 19 # x recebe o valor 19
assign ("x", 2i) # x recebe o numero imaginario 2i
#obs: o ultimo valor que x recebe é o que permanece, neste caso x=19
Apesar das diferentes formas de atribuição mostradas acima. Utilizaremos nessa apostila, por uma questão de precedência de operadores, sempre os símbolos <- para atribuição de valores.
Para mostrar o valor armazenado em uma variável, basta digitar a variável no Console e apertar Enter. Qualquer valor digitado sem atribuição pode ser mostrado na tela.
x <- 50 # x recebe o valor 50
x/20 # x dividido por 20
x <- 10:20 # cria uma sequencia de números de 10 a 20
x[1:5] # mostra os 5 primeiros números da sequencia criada
y <- sum((10:20)^2)==sum(x^2)
y
x <- seq(0, 50, l = 101) # cria uma sequencia de 0 a 50 com 101 números
y <- 1 - (1/x) * sin(x) # cria um valor para y
plot(x,y, type = "l", col = "blue") # constrói um gráfico com as variáveis x e y na cor azul
install.packages() # Instalar pacotes
library() # Loads packages
c() list() # Construir vetor; Listar vetor
data.frame() # Construir data.frames
x:y seq(x,y,...) # Criar vetor entre valores x e y
getwd() # Mostrar o diretorio atual
setwd() # Definir o diretorio de trabalho
dir() # Listar os arquivos no diretorio de trabalho
? # Buscar ajuda
read.table() read.csv() read.delim() # Importar dados
colnames() # Informar ou aplicar nomes em vetores
head() tail() # Informar primeiro é ultimo dado em um data.frame
summary() aggregate() table(x) addmargins(table(x)) prop.table(table(x), 1:2) # Estimar tabelas estatisticas
x[i], x[i, j], x$j # Extrair ou aplicar a elementos de matrizes e data.frames
plot(y ~ x) hist(y) boxplot(y ~ x) # Gerar graficos
na.omit() # omitit missins
Exemplos:
#setwd("C:/Rcurso 2020") ## definir pasta de trabalho
getwd() # mostrar pasta de trabalho
x <- seq(0, 50, l = 101)
y <- 1 - (1/x) * sin(x)
mean(x) # media de x
mean(y) # media de y **vai dar NaN
mean(y, na.rm=TRUE) # media de y, removendo NaN
# remover Na NaN
mean(na.omit(y))
sum(y, na.rm = TRUE)
cor(x[2:50], y[2:50])
2.5 Operações matemáticas simples¶
As operações matemáticas simples que podem ser executadas no R são:
- potenciação (^);
- divisão (/);
- divisão inteira ( % / %) - retorna o quociente inteiro da divisão;
- divisão resto (%%); - retorna o resto da divisão
- multiplicação (∗);
- adição (+);
subtração (-)
Exemplo:
x = 9.8*(36/10)
x = 40+ x*(40-x)
x
20 / 3
20 %/% 3 # retorna o quociente inteiro da divisao
20 %% 3 # retorna o resto da divisao
x <- 4
y <- 3
x+y; x-y; x*y; x/y; x^y; x**y; x%/%y; x %% y # Operadores aritmeticos
1!=2; 1!=1; 1&2<=1; 1&2>0; 1|2!=1; 1|2==1 #TRUE OR FALSE?
cat("verificar variável")
x <- 1
y <- -1
x<y; x>y; x<=y; x>=y; x==y; x!=y; # Operadores relacionais
cat("verificar valor em vetor")
x <- 1
Y <- -1:1
x%in%Y
x>Y
x <- c(3,0); # cria objeto
(2<=x)&(4>=x) #3 é maior ou igual a 2? e 4 é maior ou igual a 0?
(x<=1)|(x==4)
x <- c(TRUE, TRUE, FALSE, FALSE)
y <- rep(TRUE,4)
z <- rep(FALSE,4)
nx <- c( FALSE, FALSE,TRUE, TRUE)
# Operadores logicos
cat("___ou___")
x&y;
x&&y; x&&z; y&&z; x&&nx;
cat("___e___")
x|y;
x||y; x||z; y||z; z||FALSE;
2.7 Funções matemáticas simples¶
Algumas chamadas de funções matemáticas simples.
- abs(x) # valor absoluto
- log(x,b) # logaritmo de x com base b
- log(x) # logaritmo natural de x
- log10(x) # logaritmo de x com base 10
- exp(x) # exponencial elevado a x
- sin(x) # seno de x
- cos(x) # cosseno de x
- tan(x) # tangente de x
- round(x, digits = n) # arredonda x com n decimais
- ceiling(x) # arredondamento de x para o maior valor
- floor(x) # arredondamento de x para o menor valor
- length(x) # numero de elementos do vetores
- sum(x) # soma dos elementos do vetor x
- prod(x) # produto dos elementos do vetor x
- max(x) # seleciona o maior elemento do vetor x
- min(x) # seleciona o menor elemento do vetor x
- range(x) # retorna o menor e o maior elemento do vetor x
3 Objetos básicos¶
O R é orientado a objetos. Os tipos básicos de objetos são: vetores, matrizes, dataframes, listas e funcões. Nessa seção aprenderemos um pouco mais sobre essas estruturas de dados e alguns comandos básicos para manipulá-las. É importante salientar que muitas funções são orientadas especificamente a natureza do objeto, assim uma mesma função pode retornar saídas diferentes dependendo da natureza do objeto, mas é mais comum existir funções que são exclusivas a uma natureza específica, levando ao erro caso da função caso a definição do objeto seja diferente da demandada pela função.
3.1 Vetores¶
Vetores são uma sequências de valores numéricos ou de caracteres(letras, palavras). Sua principal utilidade é poder armazenar diversos dados em forma de lista e aplicar funções e operações sobre todos os dados pertencentes a determinado vetor com apenas poucos comandos.
Exemplo:
vec1 <- c(1,4,10,13.10,91,15.8) #forma mais simples de declarar um vetor
vec1
vec2 <- 1:6 # cria um vetor com uma sequencia de 1 ate 6
vec2
vec3 <- c((1:3),(3:1))
vec3
vec4 <- c(0,vec3[1:2], vec3[5:6] , 0)
vec4
seq(from = 1, to = 8) # vetor de 1 ate 8
seq(from = 1 ,to = 15, length.out = 3) #vetor de 1 ate 15 com 2 elementos
seq(from = 1 , to = 15, by = 3) #vetor de 1 ate 15 com passo 2
rep(10, 3) # repete o elemento 10, dez vezes
rep(3:4, 2) #repete a sequência de 3 a 6, três vezes
3.2 Arrays¶
Podemos definir arrays como um conjunto de elementos de dados, geralmente do mesmo tamanho e tipo de dados. Elementos individuais são acessados por sua posição no array. A posição é dada por um índice, também chamado de subscrição. O índice geralmente utiliza uma sequência de números naturais. Arrays podem ser de qual- quer tipo, porém neste capítulo abordaremos apenas arrays numéricos, devido a sua grande importância para declaração de matrizes. Existem arrays unidimensionais e multi- dimensionais. Arrays numéricos unidimensionais nada mais são do que vetores, como já vimos. Já arrays numéricos multidimensionais podem ser usados para representação de matrizes.
Exemplo:
# x <- array (dados, dim = vetor_dimensao) #sintaxe
x <- array(c(10:20), dim = c(2,2))
x
Obs: Vetores são arrays de uma dimensão. Já Arrays podem ser definidos com quantas dimensões o usuário desejar.
x <-matrix(data = dados, nrow = m, ncol = n, byrow = Q) #sintaxe- "m" = numero de linhas,
- "n" = numero de colunas
- se Q = 1 #ativa disposicao por linhas
- se Q = 0, mantem disposicao por colunas
M <- matrix(c(21:28), 2,4 ) # matriz com uma sequencia de 21 a 28, de 2 linhas e 4 colunas
M
M[1,3] # retorna o elemento que se encontra na linha 1 e coluna 3
M[2,1:2] # retorna todos os elementos da linha 2
Operações e funções matriciais¶
Abaixo segue uma tabela com as principais operações e funções realizadas entre matrizes para algebra linear.
- A*B # produto elemento a elemento de A e B
- A%*%B #produto matricial de A por B
- A %o% B # AB'
- crossprod(A,B) # t(A)%*%B
- tcrossprod(A,B) # A%*%t(B)
- crossprod(A) # t(A)%*%A
- A = aperm (A) # matriz transposta
- A = t(A) # matriz transposta
- B = solve(B) #matriz inversa B = B^{-1}
- x = solve(A,b) #resolve o sistema linear Ax = b
- det(C) # se C é matrix...retorna o determinante de C
- diag(v) # se v é vetor...retorna uma matriz diagonal onde o vetor v é a diagonal
- diag(A) # se A é matrix...retorna um vetor que é a diagonal da matriz A
- diag(n) # se n é um inteiro, retorna uma matriz identidade de ordem n
- eigen(A) # retorna os autovalores e autovetores de A
- svd(A) # Decomposição em valores singulares
- chol(A) # Decomposição de Choleski
n = 5
A=matrix(rnorm(n*n, 0, 2) , n , n)
v = c(1:10)
diag(v)
diag(A)
diag(n)
M <- matrix(c(1,2,3,5,7,11,13,17), 2,4 )
A <- M%*%t(M)
B <- t(M)%*%M
C <- kronecker(t(M), M) # == t(kronecker(M, t(M)))
D <- replicate(8,"_|_")
D<- cbind(rbind(A, matrix("-",6,2) ),D,rbind(B,matrix("-",4,4)),D,C)
colnames(D)<- c("A1", "A2", "T", "B1", "B2","B3", "B4","T", "C1", "C2","C3", "C4", "C5", "C6","C7", "C8" )
D
# rbind() # juntar matrizes verticalmente
# cbind() # juntar matrizes horizontamente
Resolver o sistema de equações:
- x + y =0
- y + 4z =1
- y + 2z =5
b <- array(c(0,1,5), dim = c(3,1))
C <- matrix(c(c(1,1,0),c(0,1,4),c(0:2)),3,3,1) # 1 linhas 0 colunas (0 é o padrão)
R = solve(C,b)
matrix(c("x","y","z", R) ,3,2)
- rowSums(a) - Soma de elementos das linhas da matriz
- colSums(a) - Soma de elementos das colunas da matriz
- rowMeans(a) - média das linhas
- colMeans(a) - média das colunas
A <- matrix(c(1,2,3,4),2,2)
matrix(c(colMeans(A),
colSums(A),
rowSums(A),
rowMeans(A)), 2,4)
B <- D[,c(9,13,10,14,11)]
class(B) <- "numeric"
B <- B[B[,1]<10,]
B[1,4] <- B[2,3]
B[4,1] <- B[3,2]
B
det(B)
round(solve(B),5)
3.4 Listas¶
Listas são conjuntos de objetos de "qualquer" natureza no R, como vetores, data frames, matrizes, scalares ou até mesmo listas. Não precisam ter o mesmo tamanho ou a mesma natureza.
a = list(A = 1, "b", 34, c(1,2,3,4), f = function(x){x^2})
a$f(2)
a
3.5 Data frames¶
Data frames também são coleções de vetores, mas aceitam vetores de tipos diferentes (numéricos e caracteres). Normalmente, guardamos dados em objetos do tipo data frame, pois sempre temos variáveis numéricas e variáveis categóricas, por exemplo, nome do aluno e idade do aluno, respectivamente. Desse modo, essa estrutura proporciona mais liberdade para manipulação de dados.
Com a função data.frame reunimos vetores de mesmo comprimento em um só objeto:
dataframe <- data.frame() #sintaxe
Exemplo:
df <- data.frame (ipca = c(6.62, 4.61,6.03,5.28, 5.70),
selic = c(1.46, 1.15, 1.16, 1.21, 1.24))
df[1:2,]
Transformando outros objetos em um data.frame com a função as.data.frame()
ipca <-c(6.62,4.61,6.03,5.28, 5.70) # cria objeto
selic <- c(1.46,1.15,1.16,1.21,1.24)
nivel_emprego <- c(159.1473,158.0703,156.1412,152.7011,150.9488)
df2 <-data.frame (ipca ,selic , nivel_emprego ) #criando data.frame com os objetos dados
df2[1:3,] # mostra data.frame com as linhas de 1 a 3
O data.frame sempre terá rownames e colnames.
rownames(df2)
names(df2)
colnames(df2)<- c("ipca" , "selic", "ne")
colnames(df2)
Ordenado data.frame¶
newdf <-df2[ order ( selic ) ,] # ordenando todo o data.frame segundo a variavel selic em ordem crescente
newdf
newdf2 <-df2[ order (ipca ,selic ),]
newdf2
df2[ order (-ipca , selic ) ,]
Para remoção de uma coluna no dataframe basta atribuir NULL a coluna desejada.
Exemplo:
df$selr <- df$selic+df$ipca
df$ipca <-NULL
df
Fazer operações e agregar data frames por variáveis de grupo¶
datacsv <- read.csv2("Exemplo/Exemplo1_ipca.csv",header =T, sep=";", dec=".")
ipca <- datacsv
colnames(ipca)<- c("data", "ipca12")
ipca$ano <- floor(ipca[,1])
ipca$min <- ave(ipca$ipca12, ipca$ano, FUN = min)
ipca$max <- ave(ipca$ipca12, ipca$ano, FUN = max)
ipca$mean <- ave(ipca$ipca12, ipca$ano, FUN = mean)
ipca2 <- aggregate(x = ipca,
by = list(ipca$ano),
FUN = mean)
ipca2[1:5,];
ipca[1:5,]
Outras funções:
- names() # retorna os nomes das colunas
- with() # permite operacoes nas colunas sem repetir o nome do data.frame seguido de "$" , [ , ] ou [[]].
- sapply()# aplica uma determinada funcao nas colunas de um data.frame
- lapply() # aplica uma determinada funcao nas colunas de um data.frame , retornando uma lista
- filter() # permite filtrar apenas colunas de uma determinada classe ou referente a alguma condicao
- attach() # anexa ao conjunto de dados , de modo a poder chamar colunas diretamente
- cumsum() # a soma cumulativa de todas as entradas tomadas coluna a coluna .
- cumprod() # o produro cumulativo de todas as entradas tomadas coluna a coluna
- cummin() # retorna um vetor onde o n- esimo elemento eh o minimo de x[1] ate x[i]
- cummax() # retorna um vetor onde o n- esimo elemento eh o maximo de x[1] ate x[i]
- saveRDS() # salvar um data.frame comprimindo os dados (pode levar tempo no caso de grandes bases)
- agregate() # agregar dados segunda variavel de grupo
- subset() # selecionar partes do data frame
- merge() # juntar dois dataframes por meio de controle de codigos ou nomes de colunas ou linhas
df <- data.frame(casa = c(1:100),
festa = seq(0,1,l = 100),
util = rnorm(100),
dy = round(seq(0,1,l = 100),0)
)
tail(df)
# dividir data frame
a <- split(df$util,df$dy)
summary(a)
#Aplicar e combinar
lapply(a,mean)
#Aplicando e simplificando
sapply(a, mean)
vapply(a, mean, numeric(1))
# Dividir, Aplicar e Combinar junto
tapply(df$util, df$dy, mean)
aggregate(df$util, by=list(df$dy), mean)
aggregate(util~dy,df, mean)
e <- 5e3
x <- matrix(rnorm(e*e),e*e,1)
b <-data.frame(x)
hypot <- function(x) sqrt(x^2+x^2)
system.time({a1 <- apply(x, 2, var)})
system.time({a1 <- with(b, var(x))})
system.time({a1 <- Rfast::colVars(x)})
4 Importação de dados¶
Se os dados estiverem salvos em arquivos, sob forma de planilhas, tabelas, etc., deve- se fazer com que o R leia estes arquivos, transformando-os em um objeto. Para que o R reconheça o conjunto de dados do arquivo é necessário que as colunas sejam separadas. Caso isso não ocorra o R não conseguirá separar as colunas e emitirá uma mensagem de erro. Um modo fácil de resolver este problema é salvar a planilha de dados com o formato (.csv) que utiliza virgula (,) como elemento separador das colunas. Porém, antes de iniciar a entrada de dados no R deve-se alterar a pasta de trabalho padrão em que o arquivo de dados .csv será salvo. Para isso basta ir em :Arquivo/Mudar dir... e alterar o diretório em que será salvo o arquivo. Ao abrir a página de alteração do diretório, escolha o diretório em que será salvo o arquivo. Depois de salvar o arquivo no diretório especificado, carregue o arquivo no console do R.
Outra maneira de alterar o diretório é utilizar o seguinte comando, especificando, como argumento, o diretório requerido:
setwd('C:/Rdados') # copie o endereço do diretório,
# mas não esquece de trocar as barras \ -> /
Conferindo o diretório atualizado através do comando:
getwd ()
4.1 Importando arquivos .csv¶
De posse da pasta de trabalho e do arquivo no formato .csv na pasta Rdados, procederemos com o seguinte comando:
dir ()
Com este comando o R irá verificar se há algum arquivo na pasta de trabalho. Como previamente havíamos salvo um arquivo .csv, sabemos que o R irá encontrar este arquivo no diretório especificado anteriormente.
O primeiro consiste no arquivo "exemplo1.csv". Importaremos o exemplo1.csv, disponível na página do curso. Observe o conteúdo do arquivo e veja que ele est´a separado por vírgulas, como e típico em arquivos desse tipo. Para fazer a importação, usaremos a função read.csv2. Em seguida, devemos dar o comando para que o R carregue o arquivo .csv no console de trabalho. Para isso digite o seguinte comando:
datacsv <- read.csv2("Exemplo/Exemplo1_ipca.csv",header =T, sep=";", dec=".")
#
#datacsv <- read.table("~/Jupyter/Rcurso/Exemplo/Exemplo1_ipca.csv",header =T, sep=";" ,dec=",")
datacsv[1:5,]
Sendo:
- datacsv: é o objeto no qual os dados lidos serão reconhecidos pelo R;
- read.csv2 : função que lê o arquivo do tipo.csv.
- read.table: função que também lê arquivos do tipo.csv, mas organiza os dados em formato de tabela.
O parâmetro "header" nos permite indicar se o arquivo de dados (data.frame) tem ou não o nome nas colunas (título) na primeira linha de dados. O segundo parâmetro "sep" permite indicar o tipo de separador dos dados presentes no arquivo. Neste caso, o separador "," indica que a delimitação do campo de cada dado será feita por vírgulas. Finalmente o parâmetro "dec" permite indicar o caractere usado como separador de casas decimais dos números reais.
Observação:
existem outras sintaxes para carregar dados no console do R (verifique isso utilizando o comando “help(read.table)”), porém os argumentos permanecem idênticos aos apresentados anteriormente.
Caso o arquivo tenha título, podemos verificar o nome destes títulos através do comando:
names() # no argumento vai sempre o nome do objeto desejado
Podemos ver a dimensão do arquivo carregado por meio do seguinte comando:
dim()
`head () # retorna a primeira parte de um vetor , matriz , tabela , data frame ou funcao.'
names(datacsv);
dim(datacsv);
head( datacsv , 5) # igual datacsv[1:5 ,]
Isto porque o R, agora, considera o arquivo carregado como uma matriz ou data.frame.
Desta forma, podemos localizar linhas, colunas e elementos desta matriz. Para
isso, utilize os comandos abaixo: datacsv[1:5,] , datacsv[1,1].
Para desenvolver um exemplo com um arquivo .txt seguimos os seguintes passos:
dir() # verifica a presenca de arquivos no diretorio de trabalho
datatxt <- read.table('Exemplo/arquivoteste.txt',header=T, sep = ",", dec=".")
datatxt[1:3,]
Podemos ainda carregar um arquivo de qualquer diretório basta apenas informar este diretório no comando. Para isso, basta utilizar a sintaxe abaixo:
datatxt <- read.table('/mnt/Disco1/Jupyter/Rcurso/Exemplo/arquivoteste.txt',header=T, sep = ",", dec=".")
Vamos agora realizar um recorte no conjunto de dados. Para isso vamos usar a função subset e selecionar somente as taxas entre 2000 e 2001 para fins de comparação mais adiante.
ipca <- read.csv2("/mnt/Disco1/Jupyter/Rcurso/Exemplo/Exemplo1_ipca.csv", header = T, sep = ";", dec = ".")
ipca <- subset(ipca, data >= 2000 & data <=2015 )
colnames(ipca) <- c("data", "ipca")
data.frame(c(ipca[1:5,],datacsv[1:5,] ))
selic <- read.csv2 ("Exemplo/Exemplo2_selic.csv", header = T, sep = ",", dec = ".")
selic<- subset(selic, data >=2000 & data <=2015 )
nivel_emprego <- read.csv2 ("Exemplo/Exemplo3_nivelemprego.csv", header = T, sep = ";", dec = ".")
nivel_emprego <- subset(nivel_emprego, data >=2000 & data <=2015 )
dados <- data.frame (selic , ipca , nivel_emprego)
Salvando os dados em um arquivo.txt via write.table() e arquivo csv via a função write.csv().
contudo é possivel salvar um arquivo csv usando write.table() ou o contrário.
write.table(dados, "Exemplo/dados.csv", sep = ";")
write.csv(dados, "Exemplo/dados.txt")
x <- runif(1000000)
x[sample(1000000, 900000)] <- NA # 10% NAs
df3 <- as.data.frame(replicate(100, x))
a <- dim(df3)
save(df3, file = "Exemplo/EXEsave.Rdata") # save.image() salva todo espaço de trabalho
saveRDS(df3, "Exemplo/EXEsave.RDS")
write.csv(df3, 'Exemplo/EXEsave.csv') # write.csv2 write.table
feather::write_feather(df3, 'Exemplo/EXEsave.feather') # eficente python-R data
foreign::write.dta(df3, 'Exemplo/EXEsave.dta') # Stata V<=13
haven::write_dta(df3, 'Exemplo/EXEsave2.dta') # Stata V>=14 (le versões anteriores com erro em acentos)
load("Exemplo/EXEsave.Rdata")
readRDS("Exemplo/EXEsave.RDS")
read.csv('Exemplo/EXEsave.csv') # read.csv2 read.table
feather::read_feather('Exemplo/EXEsave.feather')
foreign::read.dta('Exemplo/EXEsave.dta')
haven::read.dta('Exemplo/EXEsave.dta')
| formato | user | system | elapsed | size | N | K |
|---|---|---|---|---|---|---|
| Feather | 0.736 | 0.932 | 5.630 | 774.86774 | 1e+06 | 100 |
| Stata13 | 4.888 | 1.011 | 10.967 | 762.95501 | 1e+06 | 100 |
| Stata14 | 11.385 | 1.279 | 18.160 | 763.00102 | 1e+06 | 100 |
| RDS | 12.107 | 0.113 | 12.700 | 74.03126 | 1e+06 | 100 |
| Rdata | 12.288 | 0.111 | 12.907 | 74.03125 | 1e+06 | 100 |
| CSV | 36.440 | 0.734 | 42.128 | 437.62616 | 1e+06 | 100 |
| formato | user | system | elapsed | size | N | K |
|---|---|---|---|---|---|---|
| Feather | 0.878 | 0.218 | 1.122 | 774.86774 | 1e+06 | 100 |
| RDS | 2.073 | 0.024 | 2.097 | 74.03126 | 1e+06 | 100 |
| Rdata | 2.124 | 0.186 | 2.311 | 74.03125 | 1e+06 | 100 |
| Stata13 | 3.163 | 0.310 | 3.473 | 762.95501 | 1e+06 | 100 |
| Stata14 | 12.713 | 0.397 | 13.238 | 763.00102 | 1e+06 | 100 |
| CSV | 17.664 | 0.397 | 18.060 | 437.62616 | 1e+06 | 100 |
5 Tabelas e estatísticas¶
5.1 Estatísticas descritivas¶
- Média: A média aritmética é igual ao quociente entre a soma dos valores do conjunto e o número total dos valores.
- Mediana e quartil: A mediana e quartil são medidas de posição segundo uma ordem (geralmente crescente).
- Moda: É o valor que ocorre com maior frequência no conjunto de dados
- Máximo e Minimo: Para calcular amplitudes, máxima e mínima é preciso usar as funções max() e min().
- Variância e desvio padrão:medidas de dispersão calculadas a partir do desvio da média.
v <-c(1 ,2 ,1 ,2 ,2 ,3 ,2) # cria objeto
x <- c (8 ,16 ,15 ,2 ,19 ,28 ,89 ,50 ,91)
y <- c (2 ,8 ,19 ,15 ,15 ,15 ,89 ,91)
z <- c(5 ,3 ,15 ,0 ,3 ,8 ,1 ,19 ,50)
mean(x) # retorna a media
median(z) # retorna a mediada
quantile(x)
max(y) # retorna o maior valor do conjunto
min(y) # retona o menor valor do conjunto
range(z)
max(y)-min(y)
diff(range(z))
var(v) # variancia
sd(v) # desvio-padrão
summary(z)
5.2 Tabelas¶
Tabelas são uma forma resumida de apresentar estatisticas ou caracteristicas dos dados. O objetivo é apresentar os dados e podem ser muito úteis em análises econômicas.
As tabelas são feitas de acordo com a natureza da variável. Para variáveis discretas são comuns tabelas de frequencia e percentagem. Para variáveis contínuas são mais comuns tabelas de estatísticas com medidas de tendência central ou de disperção dos dados.
Tabelas de variáveis discretas¶
#library("haven") # read_dta() stata <=13
library("foreign") # read.dta() stata>=14
pnad <- read.dta('Exemplo/pnad_mod.dta')
table(pnad$raca)
table(pnad$sexo)
table(pnad$sexo, pnad$raca)
table(pnad$sexo, pnad$raca, exclude=c("Amarela", "n/d", "Ind\xedgena"))
pnad$raca <- droplevels(pnad$raca) # deletar levels em que não exite informação
attach(pnad) # comando para referenciar variaveis do dataframe diretamente
#detach(pnad, pos = 1) # retirar data frame de referencia pode ter mais de um data.frame em referencia a pos a ordem deles
prop.table(table(sexo, raca),1)
prop.table(table(sexo, raca),2)
prop.table(table(sexo, raca),1)
prop.table(table(sexo, raca))
Tabela de variáveis contínuas¶
tapply(idade,sexo,mean)
d <- data.frame(tapply(idade,raca, mean)) # tapply não funciona se existir label factor sem valores
d[2] <- data.frame(tapply(idade,raca, median))
d[3] <- data.frame(tapply(idade,raca, sd))
d[4] <- data.frame(tapply(idade,raca, min))
d[5] <- data.frame(tapply(idade,raca, max))
colnames(d) <-c("Idade", "mediana", "sd", "minimo", "maximo")
d
d <- data.frame(tapply(renda,raca, mean, na.rm = TRUE)) # tapply não funciona se existir label factor sem valores
d[2] <- data.frame(tapply(renda,raca, sd, na.rm = TRUE))
d[3] <- data.frame(tapply(renda,raca, quantile, na.rm = TRUE))
colnames(d) <-c("Renda", "desvio", "Quartis")
d
pnad$ren_fam[pnad$ren_fam>=999999] <-0 # missings do ibge são referenciados com digitos nove
pnad2 <-subset(pnad, idade>=20)
pnad2$sexo<-as.numeric(pnad2$sexo)
pnad2$raca<-as.numeric(pnad2$raca)
tabpnad <- dplyr::select_if(pnad2, is.numeric)
tabpnad <- na.omit(tabpnad)
tabpnad[1:2,]
tabpnad<- aggregate(tabpnad[,2:11],
by = list(tabpnad$sexo, tabpnad$raca),
FUN = mean)
tabpnad$Group.1 <- factor(tabpnad$Group.1,
levels = c(1,2),
labels = c("Mulher", "Homem"))
tabpnad$Group.2 <- factor(tabpnad$Group.2,
levels = c(1,2,3),
labels = c("Branco", "negro", "pardo"))
tabpnad[1:6,]
5.3 Estatística multivariada¶
Esta subseção tem apenas o perfil introdutório Fellipe Gomes e Ralph Silva tem trabalhos mais aprofundatos para quem quer ingressar mais intensamente em multivariada.
É fundamental conhecer o pacote MVar.pt que lista todos os principais modelos em multivariada.
Base para maioria dos modelos de BIGDATA e aprendizado de máquina por meio de algortimos, seu uso permita extrair informações de grandes dados computacionais.
Os modelos básicos são a Análise Fatorial e Análise de Componentes Principais, por serem básicos não é necessário pacotes adcionais para estes dois modelos, entre as vantagens:
- Permite analisar fatores que não são diretamente observáveis (variáveis latentes), com base em um conjunto de variáveis observáveis.
- Reduzir a dimensão dos dados quando existem um número elevados variáveis (correlacionadas) observadas a um conjunto reduzindo de fatores (não correlacionados).
Além das possibildiades analíticas, seus resultados podem ser empregados em outros modelos como regressões, atravéz dos escores das variáveis, cargas fatoriais ou dos fatores para aumentar eficiência do modelo.
Bibliotecas:
#library(ggfortify) # Data Visualization Tools for Statistical Analysis Results
# library(MVar.pt) # similar a MVar, com saídas em português
# https://cran.r-project.org/web/packages/MVar.pt/MVar.pt.pdf
# library(MASS) # Support Functions and Datasets for Venables and Ripley's MASS
library("haven") # ignore labels pull numbers
pnad <- read_dta('Exemplo/pnad_mod.dta')
summary(pnad)
# correções
pnad$V4617 <- NULL
pnad$V4618 <- NULL
pnad$migra <- NULL
pnad$uf <- NULL
pnad$infantil<- NULL
pnad$ocup <- NULL
pnad$renda <- NULL
pnad$lnrenda <- NULL
pnad$masc <- NULL
pnad$branco <- NULL
pnad$raca <- NULL
pnad$ren_fam <- ifelse(pnad$ren_fam>=999999,0,pnad$ren_fam)
pnad$per_capita <- ifelse(pnad$per_capita>=999999,0,pnad$per_capita)
pnad<- na.omit(pnad)
summary(pnad)
corPNAD <- round(cor(pnad),4) # 4 casas decimais
corPNAD
library(ggplot2)
library(ggcorrplot)
ggcorrplot(corPNAD, hc.order = TRUE, type = "lower", lab = TRUE, lab_size = 2, method="circle", colors = c("red", "white", "green"), title="Correlação PNAD")
Análise fatorial
factanal(x, factors, data = NULL, covmat = NULL, n.obs = NA,
subset, na.action, start = NULL,
scores = c("none", "regression", "Bartlett"),
rotation = "varimax", control = NULL, ...)##### Analise fatorial (maxima verossimilhanca)
AF <-factanal(pnad, factors = 5) # 3 exige um numero de vetores independentes >=3
AF
table(pnad$sexo)
# cargas fatorias
L1 <- AF$loadings[,1]
L2 <- AF$loadings[,2]
U <- AF$uniquenesses
# Rotacao de fatores
AFmax <- factanal(pnad,factors=2,rotation="varimax")
AFmax
# Escores fatoriais
AFReg <- factanal(pnad,factors=2, rotation = "varimax",scores="regression")
AFBar <- factanal(pnad,factors=2, rotation = "varimax",scores="Bartlett")
par(mfrow=c(2,1))
plot(AFReg$scores[,1],AFBar$scores[,1])
plot(AFReg$scores[,2],AFBar$scores[,2])
Análise de Componentes Principais
## Formúla
prcomp(formula, data = NULL, subset, na.action, ...)
## Padrão
prcomp(x, retx = TRUE, center = TRUE, scale. = FALSE,
tol = NULL, rank. = NULL, ...)# Análise de componentes principais:
ACP=prcomp(pnad, scale = TRUE)
summary(ACP)
ACP
# rotação
k <- 3
PCA =ACP$rotation[, 1:k] %*% diag(ACP$sdev[1:k])
CPA= varimax(PCA)
CPA
Análise gráfica
biplot(ACP)
library(ggfortify)
autoplot(ACP, label = TRUE, label.size = 3,
loadings = TRUE, loadings.label = TRUE, loadings.label.size = 3)
autoplot(AFReg, label = TRUE, label.size = 3,
loadings = TRUE, loadings.label = TRUE, loadings.label.size = 3)
Análise de cluster
Outra ferramenta importante em multivariada é a análise de cluster. Para este é necessário uma biblioteca adcional a MVar.pt...
Cluster(Data, Titles = NA, Hierarquico = TRUE, Analise = "Obs",
CorAbs = FALSE, Normaliza = FALSE, Distance = "euclidean",
Method = "complete", Horizontal = FALSE, NumGrupos = 0,
Casc = TRUE)Distance: Metrica das distancias caso agrupamentos hierarquicos: "euclidean" (default), "maximum", "manhattan", "canberra", "binary" ou "minkowski". Caso Analise = "Var" a metrica sera a matriz de correlacao, conforme CorAbs.
Method: Metodo para analises caso agrupamentos hierarquicos: "complete" (default), "ward.D", "ward.D2", "single", "average", "mcquitty", "median" ou "centroid".
library(MVar.pt)
pnad2<-pnad[1:600,c(1,2,4,7,10)]
Res <- Cluster( pnad2, Analise = "Obs", CorAbs = TRUE,
Normaliza = TRUE, Horizontal = FALSE, NumGrupos = 3, Hierarquico = TRUE,
Distance = "manhattan", Method = "ward.D")

print("Tabela com as similaridades e distancias:"); Res$TabRes
print("Grupos formados:");table(Res$Groups$Grupos)
print("Tabela com os resultados dos grupos:"); Res$ResGroups
print("Soma do quadrado total:"); Res$SQT
#print("Matriz de distancias:"); Res$MatrixD
#write.table(file="Exemplo/TabelaSimilaridade.csv", Res$TabRes, sep=";",dec=",",row.names = FALSE)
5.4 Funções e estruturas de controle e repetição¶
5.4.1 Funções¶
Não é raro a necessidade de escrever funções simples a fim de simplificar rotinas de trabalho. Apesar do R ter um número elevado de pacotes e funções, instalar pacotes para rotinas relativamente simples pode ser desnecessário. Podendo o próprio usuário construir a sua função. A estrutura básica:
personalfunction<-function(argumentos){`expressão'
saída
}
Exemplos
estattabble<-function(x) {
a1 <- mean(x)
a2 <- median(x)
a3 <- sd(x)
a5 <- max(x)
a4 <- min(x)
d <- data.frame(c(a1,a2,a3,a4,a5))
rownames(d) <-c("Média", "mediana", "sd", "minimo", "maximo")
colnames(d) <-c("estatisticas da variável")
d
}
estattabble(ipca$ipca)
esfera<-function(raio) {
V = (4/3)*pi*raio^3
A = (4)*pi*raio^2
d <- data.frame( c(V,A))
rownames(d) <-c("Volume", "Área")
colnames(d) <-c(paste("Para esfera de raio ",raio,":"))
d
}
circulo<-function(raio) {
C = 2*pi*raio
A = pi*raio^2
d <- data.frame( c(C,A))
rownames(d) <-c("Circunferência", "Área")
colnames(d) <-c(paste("Para o circulo de raio ",raio,":"))
d
}
esfera(2)
circulo(2)
Equação Black-Scholes¶
A equação de Black-Scholes descreve o preço de uma opção ao longo do tempo. Por exemplificação, usaremos a fórmula final definida por:
\begin{equation} \mathrm C(\mathrm S,\mathrm t)= \mathrm N(\mathrm d_1)\mathrm S - \mathrm N(\mathrm d_2) \mathrm K \mathrm e^{-rt} \label{eq:2} \end{equation}\begin{equation} \mathrm d_1= \frac{1}{\sigma \sqrt{\mathrm t}} \left[\ln{\left(\frac{S}{K}\right)} + t\left(r + \frac{\sigma^2}{2} \right) \right] \end{equation}\begin{equation} \mathrm d_2= d_1 - {\sigma \sqrt{\mathrm t}} \end{equation}\begin{equation} N(x)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} \mathrm e^{-\frac{1}{2}z^2} dz \label{eq:5} \end{equation}Notação:
- C = Preço da opção de compra (call.price)
- S = Preço atual da opção (stock.price)
- K = Preço de exercício da opção (strike.price)
- t = tempo para a maturidade da opção em anos (years.maturity > 0)
- r = taxa de juros livre de risco (risk.free
[0,1]) - $\sigma$ = volatilidade do retorno das ações (volatility )
- N = função de distribuição acumulada normal
# Black sholes
#S= stock.price
#K= strike.price
#t= years.maturity
#r= risk.free rate
#v= Volatility (desvio padrão)
Black.Scholes <- function(S,K,t,r,v) {
d1 <- (log(S/K)+t*(r+(v^2)/2))/(v*sqrt(t))
d2 <- d1-v*sqrt(t)
cp = S*pnorm(d1)-pnorm(d2)*K*exp(-r*t)
pp = K*exp(-r*t)*pnorm(-d2)-S*pnorm(-d1)
tb <- data.frame(c( cp,pp,d1,d2))
rownames(tb) <- c("call.price", "put.price", "d1", "d2")
tb
}
Black.Scholes(10,12, 1, .06, 2)
5.4.2 Estruturas de controle¶
Em programação, controles são estruturas que permitem controlar o fluxo de um programa, as estruturas básicas são:
if e else: para testar condições lógicas;
if(x > 3) {y <- 10 } else { y <- 0 } y <- if(x > 3) { 10 } else { 0 }
ifelse() : para testar condições lógicas;
ifelse(x > 3, TRUE, FALSE) ifelse(x > 3, X<- 3, x <- 0)
x <-5
if(x > 3) {
y <- 10
cat(y)
} else {
y <- 0
cat(y)
}
y <- ifelse(x > 3,10,0)
cat(y)
y1 <- if(x > 3) { 10 } else { 0 }
y2 <- ifelse(x > 3, 10 , 0 )
y1==y2
5.4.3 Estruturas de repetição¶
Por vezes serão necessários repetir comandos, linhas de comandas ou mesmo funções.
Na maioria das vezes será muito melhor que esta repetição seja feita por estruturas de repetição ao invez de escrever o mesmo comando repetidamente.
- for: quando o loop tem um número fixo de repetições:
for(i in 1:10) { print(i)}` x <- c("a", "b", "c", "d"); for( y in x) {print(y)}
- while: quando não se sabe a dimenssão do loop:
x <- 1000; while(x < 10000) { print(x) x <- x + 1000 }
- repeat: similar a while, repete de forma infinita até que a função break seja executada;
break: permite sair de qualquer tipo de loop;
x<- 1 y<- 2 repeat { xi<- rnorm(1) if(abs(xi - x) >y) { break }else { x<- xi } }
- next: ignora a interação de um loop;
for(i in 1:100) { if(i > 2 & i< 10 ) { ## não executa ações no loop 3 a 9 next } ## execução }
Estas estruturas são utilizadas com frenquência em rotinas de programação, mas não são as únicas, apenas as mais relevantes neste curso.
boletim <- function(){
cat("precione enter uma vez para o próximo nome ou duas vezes para finalizar")
nomes <- scan(what = "character")
cat("precione enter uma vez para a próxima nota ou duas vezes para finalizar")
notas <- scan()
a<- length(notas)
notas <- data.frame(nomes, notas)
for (i in c(1:a)) {
notas[i,3] <- ifelse(notas[i,2]>= 70, "Aprovado", "Reprovado")
notas[i,4] <- ifelse(notas[i,2]>= 70, "C","R")
notas[i,4] <- ifelse(notas[i,2]>= 80, "B", notas[i,4])
notas[i,4] <- ifelse(notas[i,2]>= 90, "A", notas[i,4])
}
names(notas) <- c("Aluno", "Nota", "Status", "Conceito")
print(notas)
}
Exercício.¶
Reescreva a função boletim() trocando a estrtura de repetição "for" por "while" e depois por "repeat".
5.4.4 Transformando, aplicando, replicando tabelas e matrizes¶
A família de funções "apply" tem como objetivo replicar, de maneira eficiente, ações em diferentes objetos. É quase sempre uma alternativa mais rápida e eficiente ao clássico loop quando estamos trabalhando com matrizes, tabelas e listas.
Funções da família apply:
- apply()
- mapply()
tapply()
lapply()
- sapply()
- vapply()
- rapply()
funções relacionadas
- rep()
aggregate()
Sweep()
apply
Replica determinada função por linha ou coluna de uma array.
A1 <- matrix(round(runif(25)*10,0), nrow=5, ncol =5 )
A1
apply(X = A1,MARGIN = 1, FUN = mean)
mean(A1[2,])
apply(A1,2, mean)
mean(A1[,3])
- rep
Replica um objeto (básico) determinadas vezes.
rep(1,5)
rep("casa",5)
rep(1:5,2)
6*4*2+5*4+10
- mapply
Aplica derterminada a função a todos os elementes de um ou mais objetos do tipo matriz ou tabela.
mapply(sqrt,A1)
mapply(rep,1:5,5)
mapply(function(x, y) x^2+y,
c(1, 2, 3),
c(4, 5, 6))
mapply(function(x, y) c(x^3, y^2),
c(1, 2, 3),
c(4, 5, 6))
- tapply
Aplica determinada função a um conjunto de dados (matrix, data.frame) condicionados a outra variável.
n<- 20
fac <- data.frame(sexo = factor(rep_len(1:2, n), levels = 1:2, labels = c("Homem", "Mulher")),
renda = round(rnorm(20,2000,50),2)
)
table(fac$sexo)
tapply(fac$renda, fac$sexo, sum)
library(foreign)
pnad <- read.dta('Exemplo/pnad_mod.dta')
pnad2 <- pnad[,c(18,3,8,13,21)]
pnad2 <- na.omit(pnad2)
pnad2[1:5,]
pnad2 <- na.omit(pnad2)
result <- lm(pnad2, lnrenda =~ idade+educ+componentes+negro)
# estraindo estaísticas dos resultados
summary(result)
DegreesOfFreedom <- result$df
Yhat <- result$fitted.values
Coef <- result$coefficients
Resid <- result$residuals
RSquared <- result$r.squared
aic <- AIC(result)
bic <- BIC(result)
Outros modelos em Cross Sectional data podem ser estimados pelo comando glm(). Como segue na tabela abaixo.
GLM Family link
| Family | identity | logit | probit | cloglog | sqrt | inverse | log | 1/mu² | cauchit |
|---|---|---|---|---|---|---|---|---|---|
| gaussian | sim* | - | - | - | - | sim | sim | - | - |
| binomial | - | sim* | sim | sim | - | - | sim | - | sim |
| poisson | sim | - | - | - | sim | - | sim* | - | - |
| Gamma | sim | - | - | - | - | sim* | sim | - | - |
| inverse.gaussian | sim | - | - | - | sim | sim | sim | sim* | - |
| quasi | sim | sim | sim | sim | sim | sim | sim | sim | - |
variance link option: "constant", "mu(1-mu)", "mu", "mu^2", "mu^3", "Binomial()", "binary", "NegativeBinomial()", nbinom
Para mais opções ver glmer e brms.
pnad2$dr<-pnad2$lnrenda>mean(pnad2$lnrenda)
table(pnad2$dr)
h <- glm(dr~idade+educ+componentes+negro, data = pnad2, family=binomial(link="logit"))
summary(h)
Podemos montar nossa própria regressão manualmente
MQO = function(T) {
# Curso introdução ao R Econs
# Por: ANDRE SURIANE
# UFJF
# Faculdade de Economia
# laboratório de estudos econômicos Econs
# estimar uma regressão linear simples passo a passo
# T é um data frame em que a primeira coluna é a variável a dependente e todas
# as demais são explicativas <<não deve conter a constante>>
T <- na.omit(T)
N <- nrow(T) # numero de linas
K <- ncol(T) # numero de variaveis
DEP <- as.matrix(T[1]) # variavel dependente
intercept <- matrix(1, nrow = N) # constante
X <- data.frame(intercept, T[,2:K])
X <- as.matrix(X)
b <- solve(t(X)%*%X)%*%(t(X)%*%DEP) # estimativas para b do MQO
N <- nrow(T)
k <-length(b)
df <- N-K
DEPc <- X%*%b # DEPUEL calculado
er <- DEP-DEPc # erro
sigma2 <- (t(er)%*%er)/N # variancia
varR <- (t(er)%*%er)/df # variancia residual
varR <- varR[1,1]
MVC <- varR*(solve(t(X)%*%X)) # Matriz de variancia-convariancia
media <- sum(DEP)/N # media da variavel dependente
desvioT <- DEP-media # desvio total
desvioE <- DEPc-media # desvio explicado
R2 <- (t(desvioE)%*%desvioE)/(t(desvioT)%*%desvioT) # R2
erm <- (t(er)%*%er)*(N-1) # numerador dos R2 ajustado
ern <- (t(desvioT)%*%desvioT)*df # denominador do R2 ajustado
R2ajus <- 1-(erm/ern) # R2 ajustado
## critérios de ajustamento
AIC <- N*(log(2*pi)+1+log((sum(er^2)/N)))+((K+1)*2) # criterio Akaike by residuls
BIC <- AIC + K*(log(N)-2)
ll <-0.5*(sum(log(intercept))-N*(log(2*pi)+1-log(N)+log(sum(intercept*er^2)))) # likelihood function
AKI <- 2*K-2*ll # AIC by likelihood function
AICc1 <- AKI +K*(K+1)/(N-K-1)
AICc2 <- AIC +K*(K+1)/(N-K-1)
SC <- log(N)*K-2*ll # SBC by likelihood function
dp <- sqrt(diag(MVC)) # desvio padrao
et <- b/dp # estatistica T
I <- (t(desvioE)%*%desvioE)/(K-1) # numerador da estatistica F
O <- (t(er)%*%er)/(N-K) # denomindaor da estatistica F
ef <- I/O # estatistica F
pval <- 1-pf(ef,K, N) # Pvalor estatistica F
res <- data.frame(b, dp, et )
for (i in 1:K) {
res[i,4]<- 2*(min(1-pt(q=res[i,3], df=N-K), pt(q=res[i,3], df=N-K))) # Pvalor estatistica t
}
res <- round(res, 4)
colnames(res) <- c("Betas", "Des.Pad.", "Estat-t" , "P-valor")
res$signif <- ifelse(res[4]<0.001,"***", ifelse(res[4]<0.01, "**", ifelse(res[4]<0.05,"*","_")))
res2 <- data.frame(R2, R2ajus, AIC, BIC, ef, pval)
res2 <- round(res2, 4)
res3 <- data.frame(AIC, AKI, AICc1, AICc2, BIC, SC)
colnames(res2) <- c("R2", "R2ajus", "AIC", "BIC", "Esta_F", "Pvalor")
rownames(res2) <- c("Estatisticas")
return(list(res,res2,res3))
}
pnad2$dr<- NULL
MQO(pnad2)
AIC(result)
BIC(result)
6 Gráficos¶
A próxima etapa no nosso aprendizado é criar gráficos. Já vimos uma série de objetos dentro do R, mas ainda não colocamos os mesmos de forma gráfica.
Para verificar as opções de gráficos no R, acesse o link R Graph Gallery
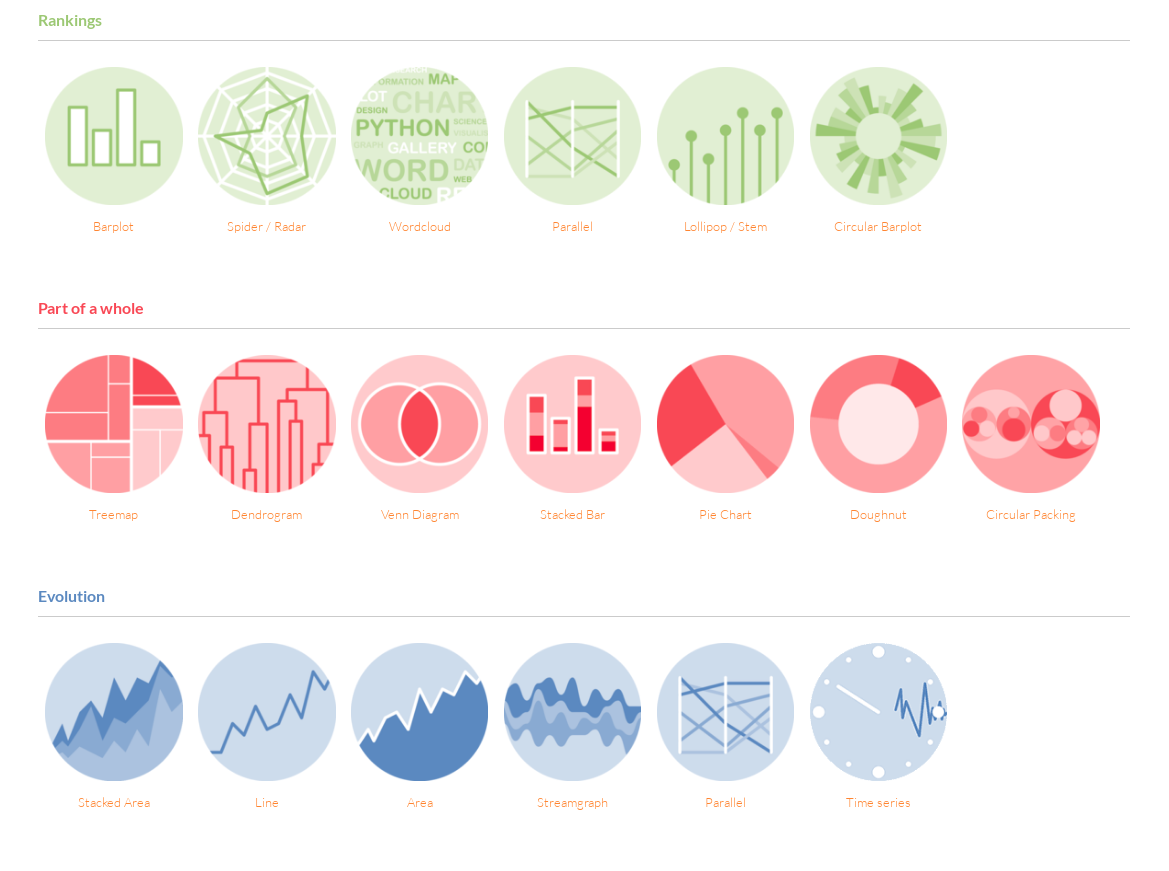
6.1 Linhas e pontos¶
O comando básico para a geração de um gráfico é o plot(). Segue abaixo o exemplo de um gráfico simples.
Exemplo:
a <- 1:30
b <- a^2
plot(a,b)
Exemplo de gráfico simples com atribuição de pontos em coordenadas cartesianas
datacsv <- read.csv2("Exemplo/Exemplo1_ipca.csv",header =T, sep=";", dec=".")
ipca <- datacsv
colnames(ipca)<- c("data", "ipca12")
ipca$ano <- floor(ipca[,1])
ipca$min <- ave(ipca$ipca12, ipca$ano, FUN = min)
ipca$max <- ave(ipca$ipca12, ipca$ano, FUN = max)
ipca$mean <- ave(ipca$ipca12, ipca$ano, FUN = mean)
ipca2 <- aggregate(x = ipca,
by = list(ipca$ano),
FUN = mean)
plot(ipca2$ano, ipca2$mean, xlab='', ylab='(%)', type='l', col='blue', main='IPCA', lwd=2, lty=1) + # l define tipo linha
lines(ipca2$ano, ipca2$min, col="darkgreen")+
lines(ipca2$ano, ipca2$max, col="red")
#Exemplo de gráfico simples para a variável IPCA.
ipca2<- subset(ipca2, ipca2$ano>1994)
plot(ipca2$ano, ipca2$mean, type="l", col ="black")+
abline(h = mean(ipca2$mean), col="purple3")
abline(h = median(ipca2$mean), col="blue")
abline(v =ipca2$ano[ipca2$mean==max(ipca2$mean)], col="darkblue")
abline(v =ipca2$ano[ipca2$mean==min(ipca2$mean)], col="blue")
Os gráficos gerados podem ser salvos imediatamente a sua criação. Existem vários formatos em que o R pode salvar essas imagens. Alguns deles são: JPEG, BMP, PDF, TIFF, PNG. No exemplo a seguir será utilizando o formato PNG, contudo a sintaxe para qualquer formato é a mesma.
png(file="Imagens/plot.png", width = 1200, height = 720, units = "px",bg = "white") # plot refere o nome da imagem
# alem de png() é possivel salvar em bmp() jpeg() tiff(), sem usar pacotes adcionais.
plot(a,b) #grafico que estamos salvando
dev.off() #fecha a janela automaticamente
Scatter plot
#attach(Z)
png(file = "Imagens/sc1.png", width = 1200, height = 720, units = "px",bg = "white")
plot( cos(x) ,cos(2*x) , cex = .5, col = "blue") +
points(sin(y),cos(2*y) , cex = .5, col = "red") +
points(x,y , cex = .5, col = "darkgreen")
dev.off()
Linhas
# Gráfico de distribuição normal com 5% de significância
# definir x e fx
x <- seq(-5, 5, l=100)
fx <- function(x) (1/sqrt(2*pi))*exp((-1/2)*(x)^2)
# plotar fx
plot(x, (1/sqrt(2*pi))*exp((-1/2)*(x)^2), ty='l')
# calcular integral
ie1 <- integrate(fx, 1.96, 5)
ie2 <- integrate(fx, -5, -1.96)
pt <- as.numeric(ie1[1])+as.numeric(ie2[1])
# definir intevalo de integração em x e valores de fx
x <- seq(1.96, 5, l=100)
fx1 <- (1/sqrt(2*pi))*exp((-1/2)*(x)^2)
# plotar integral definida de fx
polygon(rbind(cbind(rev(x),0),cbind(x,fx1)), col=adjustcolor('blue4', alpha = .6))
x <- seq(-5, -1.96, l=100)
fx2 <- (1/sqrt(2*pi))*exp((-1/2)*(x)^2)
polygon(rbind(cbind(rev(x),0),cbind(x,fx2)), col=adjustcolor('blue4', alpha = .6))
# textos
text(3, 0.05, expression(paste(integral(1/sqrt(2*pi)*e^{-(x^{2}/2)}*dx,1.96,5))), adj = 0, cex = .6)
text(-4.5, 0.05, expression(paste(integral(1/sqrt(2*pi)*e^{-(x^{2}/2)}*dx,-5,-1.96))), adj = 0, cex = .6)
#https://stat.ethz.ch/R-manual/R-devel/library/grDevices/html/plotmath.html
text(3, 0.1, paste("pv = ",round(pt,2)), adj = 0, col = "black", cex = 1)
lines(c(2.9, 2.2), c(0.1, 0.01), col = 'blue4', lwd = 2)
lines(c(2.9, -2.2), c(0.1, 0.01), col = 'blue4', lwd = 2)
exp(1)
t = 10:1000
x = sin(t/10)/(t/10)
y = cos(t/10)/(t/10)
plot(x,y,type = "l", col = "darkred") +
lines(y+.3,-x+.3, col = "darkgreen")
esferaV<-function(raio) {
(4/3)*pi*raio^3
}
esferaA<-function(raio) {
(4)*pi*raio^2
}
circuloC<-function(raio) {
2*pi*raio
}
circuloA<-function(raio) {
pi*raio^2
}
esferaA(2)
circuloA(2)
pl <- data.frame(c(1:100)/10)
pl[,2]<- circuloA(1:100/10)
pl[,3]<- circuloC(1:100/10)
pl[,4]<- esferaA(1:100/10)
pl[,5]<- esferaV(1:100/10)
colnames(pl) <- c("raio","Área círculo", "circunferência", "Área esfera", "Volume")
plot(pl[,1:2], type="l", main="esfera circulo", ylab="Volume area circunferencia")+
lines(pl[,c(1,3)], col="gray")+
lines(pl[,c(1,4)], col="blue")+
lines(pl[,c(1,5)], col="lightblue")
pl <- data.frame(c(1:100)/100)
for (i in 1:100) paste(pl[i,2]<- Black.Scholes(10,12, pl[i,1], .06, .1)[1,1])
plot(pl[,1:2], type="l", main="Black-Scholes", xlab="Tempo", ylab="Preço")
x1 <- 0:64
plot(x1, x1, type= "n")
legend("center", "(x,y)", pch = 1, title = "center")
legend("top", "(x,y)", pch = 2, title = "top, inset = .01", inset = .01, col="green")
legend("topright", "(x,y)", pch = 3, title = "topright, inset = .02", inset = .02, col="blue")
legend("right", "(x,y)", pch = 4, title = "right, inset = .04", inset = .04, col='orange')
legend("bottomright", "(x,y)", pch = 5, title = "bottomright, inset=.06", inset = .06, col='red')
legend("bottom", "(x,y)", pch = 6, title = "bottom, inset = .08", inset = .08, col="cyan")
legend("bottomleft", "(x,y)", pch = 7, title = "bottomleft, inset = .1", inset = .1, col="magenta")
legend("left", "(x,y)", pch = 8, title = "left, inset = .12", inset = .12, col="#FF004D")
legend("topleft", "(x,y)", pch = 9, title = "topleft, inset = .14", inset = .014, col="dark red")
#legend(posição, legenda, pch = "tipo de marcação [1,9]", title= "titulo", inset="deslocamento em direção ao centro, col = "cor")
6.2 Barras e histogramas¶
Um histograma divide uma série de dados em diferentes classes igualmente espaçadas e mostra a frequência de valores em cada classe. Em um gráfico, o histograma mostra diferentes barras, com bases iguais e amplitudes relativas às frequências dos dados em cada classe. O eixo das ordenadas, portanto, mostra a frequência relativa de cada classe e o eixo das abcissas os valores e intervalos das classes.
x <- rnorm(1:10000)
par(mfrow=c(2,1))
hist (x, nclass = 20) # histograma com 20 classes
hist (x, nclass = 100) # histograma com 100 classes
par(mfrow=c(2,3))
hist(idade[raca=="Branca" & sexo == "Mulher"], main = "Mulher branca")
hist(idade[raca=="Preta" & sexo == "Mulher"], main = "Mulher negra")
hist(idade[raca=="Parda" & sexo == "Mulher"], main = "Mulher parda")
hist(idade[raca=="Branca" & sexo == "Homem"], main = "Homem branco")
hist(idade[raca=="Preta" & sexo == "Homem"], main = "Homem negro")
hist(idade[raca=="Parda" & sexo == "Homem"], main = "Homem pardo")
Barras
A função barplot() gera gráfico de barras, onde cada barra representa a medida de cada elemento de um vetor, ou seja, as barras são proporcionais com a “dimensão” do elemento.
# barplot(x, col=" ", legend.text=" ", xlab=" ",ylab=" ")
x <- rnorm(1:20)
ipca3 <-c (6.62 ,4.61 ,6.03 ,5.28 , 5.70)
par(mfrow=c(2,1))
barplot(x, xlab="normal(10000)")
barplot(ipca3,xlab="IPCA variacao",col="blue") + title("IPCA")
barplot(ipca2$mean )
barplot(c(mean(pnad2$educ), mean(pnad2$componentes), mean(pnad2$lnrenda)),col="red")
barplot(c(mean(pnad$branco),mean(pnad$negro),mean(pnad$pardo),mean(pnad$masc),mean(pnad$migrante)),col="blue")
input <- matrix(c(1:100)/10, 100,1)
pl = diag(100)
for (i in 1:100) {
for (j in 1:100) {
pl[i,j]<- Black.Scholes(input[j,1], 12, input[i,1], .06, .1)[1,1]
}
}
persp(z = t(pl), xlab ="Preço das ações", ylab = "Tempo", zlab = "Preço de compra da opção", col = "red",
phi= 45,
theta = -45)
tcol <- rev(rainbow(23)[1:18])
filled.contour(t(pl),nlevel=18, col =tcol, axes = FALSE )
si = 40
data=matrix(2*rnorm(si*si)+10, si,si)
tcol <- rainbow(20)
contour(z = data, nlevel=40, col =tcol,labcex = 0.001, axes = FALSE )
